Here we consider how inertia and rotational forces can be explained as manifestations of 4D aetheric waves.

Inertia as a 4D Wave Phenomenon

Modern science doesn't have an adequate explanation of what causes inertia.
Standard theory attributes inertia to the interaction of an object with the background of all matter in the universe. This has its origin in Mach's principle which argues that if an object were alone in the universe how could it know it is being accelerated?
However, no one has been able to give a convincing explanation of how this interaction with the matter in the universe comes about.
The same arguments can be applied to rotational inertia. A gyroscope for example will maintain its direction with respect to the background of stars if it is carried around the earth and brought back to its starting point.
Again, rotational inertia seems to be tied to the background of matter comprising the universe.
One is entitled to ask what kind of interaction with the background matter is capable of keeping the gyroscope aligned to it?
The most sensible explanation for inertia is to assume an underlying medium, or aether.
Inertia can then be simply explained as some form of interaction of an object with the surrounding medium.
Another version of a possible medium has arisen out of Quantum Electrodynamics in the form of the zero point fluctuations, considered to be created spontaneously out of the 'vacuum' [1]. These represent a kind of medium that can interact with the charge components inside matter. Such interactions with matter have been proposed as an explanation for inertia [2].
However, as discussed in our Aether page, this theory has difficulty accounting for certain experiments, for which the aether makes more sense.

An aetheric model has to be able to explain inertia. Why a body traveling at constant speed feels no resistance while an accelerating one feels a strong resistance.
Again we draw on the model proposed by Maurice Cooke [3].
As discussed previously, particles of matter are formed at, and tend to remain in, the nodal points in the 4D wave pattern corresponding to low vibration regions in the aether.
Assuming that the 'primary' points generating the 4D waves move about at a whole range of speeds the nodal points will also move about at those speeds.
Therefore the atoms of a moving body have to catch a 'ride' on the nodal points moving at the same speed as the body. While they are riding on the nodal points the atoms will not experience any resistance.
However when there is a force applied to the body in order to accelerate it the atoms have to jump out of their existing nodes and onto other nodes traveling at the higher velocity.
If it is assumed that particles have a tendency to remain or 'stick' to the nodal points, we can see that jumping from one node to another will meet with some resistance. It is this resistance that we experience as inertia.
The higher the acceleration the more nodes have to be jumped per unit time and therefore the higher the resistive force.

This mechanism is also able to explain the equivalence of gravitational and inertial mass.
In the case of gravity it is the nodes that change speed and 'drag' the atoms with them, which is experienced as the gravitational acceleration (see our Gravity page). When the atoms are allowed to move with the nodes, free fall, they experience no force even though they are accelerating.
While with inertia we have the reverse situation of accelerating atoms being dragged out of their companion nodes.
In both cases the forces and accelerations will be generated by the same mechanism, resistance to jumping of nodes. Hence we can understand why gravitational and inertial masses would be equivalent.

It also follows logically that if jumping of nodes during acceleration creates a resistive force on an object there must also be a force exerted by the object on the aether.
One would therefore expect that whenever an object is accelerated there would be created some sort of movement of the aether along the direction of acceleration. The stronger the acceleration or deceleration the stronger the disturbance in the aether.
It should be possible to detect this movement by for example using techniques pioneered by Dr Kozyrev. He set up equipment that was so sensitive it was able to detect changes caused by raising and lowering a 10kg weight 2-3 meters away!
He referred to the disturbances that traveled from the weight to his detectors as torsion fields. We would simply refer to them as changes in the movement of the aether. One might also consider these as longitudinal waves with a spiral motion.
See David Wilcock's site [4] for an interesting account of Dr Kozyrev and his colleague's many discoveries.

Rotation

The above model of inertia can be used to explain the radial forces generated by the rotation of an object.
If we consider an atom at the edge of a spinning disk, Fig 6.1(a), we can see that it starts to move in a line tangential to the edge of the disk. That line of motion will not encounter any resistance as it is moving with a node which we are assuming normally travels in a straight line.
However, this can only last for a very short period before the forces that keep the wheel together pull the atom towards the centre of the disk to keep it on a circular path.
This means that the atom has to jump the node that it was moving with and temporarily follow another node that is moving tangentially to the edge of the the disk at the new atom position, Fig 6.1(b).
Because of the rapid node jumping along a line towards the centre of the disk the atom will feel a force in the opposite direction.

     
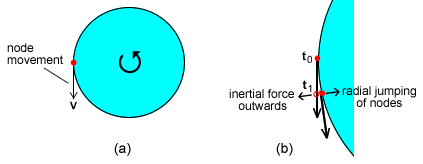
      Fig 6.1 The radial node jumping for a rotating object.

We can therefore understand why a spinning object will experience a force radially outwards but no resistance to the actual rotation (ignoring friction for the moment), in accord with experience.
And because the rate of node jumping will increase with the rate of spin, the outward force will also increase with the spin.
The conservation of angular momentum and the precessional forces on a gyroscope can be explained by a similar analysis.
One of the other consequences of the above rotation model will be a force on the aether radially towards the centre of the disk, following the action and reaction argument of the previous section.
Therefore, one would expect an increase in the aether pressure towards the axis of rotation.

However, during the initial spinning up of the disk, or while the rate of spin is increasing, there will also be some node jumping along the line tangential to the edge of the disk.
This is because the rate of spin is increasing therefore the tangential velocity v of fig 6.1(a) is also increasing. Thus there will be a resistance to the increasing of the spin rate, consistent with observation.
It also follows from this that during the spinning up there will be a force on the aether along a line tangential to the edge of the disk in the direction in which the object is spinning.
This would seem to be a reasonable mechanism by which we could explain entrainment of the aether around planetary bodies.
Indeed any spinning body would be expected to produce a spinning aether and it should be possible to detect such in the laboratory with a suitable detection mechanism such as that used by Dr. Kozyrev [4].

When we combine this rotation of the aether with the pressure towards the axis of rotation as described above we have all the elements of a spiral motion.
If we were only dealing with 3D space the inward flowing aether would have nowhere to go (except perhaps out of the north and south axis of rotation), however in 4D space the aether pressure towards the axis of rotation can push the aether into the 4th dimension.
Therefore, one would expect that the aether particles would move a short distance in 3D space before they 'disappear' into the 4th dimension, mapping out a spiral as seen from 4D space.
We have here all the elements of a vortex flow into the 4th dimension. Similar in fact to the electron vortex described in the Matter section, but with an aether circulation that is centered on an axis in 3D space.
We would therefore expect that any rotating object would create a transfer of energy from 3D space into the 4th dimension (or even higher dimensions).
This seems to be supported by unusual patterns observed at the polar regions of various planets in our solar system.
Richard Hoagland and David Wilcock have pointed out the unusual formations observed on the outer planets of our solar system [5] which are difficult to explain by standard theory. They also point out the many instances of unusual phenomena occurring at around 19.5^o latitude on many planetary bodies in our solar system.
Hoagland & Wilcock attribute these to a geometrical relationship to higher dimensions.
While our approach is different to theirs it does strengthen the proposition that rotating objects create large scale energetic flows to and from higher dimensions.

Also, as discussed on our Relativity page, we expect that when aether flows relative to matter it slows down atomic processes and therefore produces time dilation.
In the case of rotation, aether flows are more pronounced because of the strong 4D component as discussed above.
Therefore, one might expect that rapid rotation would lead to a more pronounced time dilation effect.
There is in fact experimental evidence for this.
It has been reported that Bruce DePalma carried out experiments where he spun a 30 pound concrete disk at some 8000 rpm.
Above the disk he suspended a Bulova Accutron watch that according to the specifications was accurate to within 1 second per year. However, the watch above the spinning disk reportedly lost 1 second in 20 minutes!

References

[1] Thomas Valone, “Understanding Zero Point Energy", users.erols.com/iri/ZPEpaper.html
[2] Haisch B., Rueda A., Puthoff H.E., “Physics of the zero-point field: implications for inertia, gravitation and mass", Speculations in Science
     and Technology, 20, 99-114 (1997), copy available at   www.earthtech.org/publications/spec_sci_tech.pdf
[3] Maurice B. Cooke, “Einstein Doesn’t Work Here Anymore”, Marcus Books, PO Box 327, Queensville, Ontario, Canada L0G 1R0, 1983
[4] David Wilcock, “Divine Cosmos",  www.divinecosmos.com
[5] R. Hoagland and D. Wilcock, "Interplanetary Day After Tommorow",  www.enterprisemission.com

Go to Top